Floating-point format and Mixed Precision in TensorFlow19 May 2022 / 11 minutes to read Elena Daehnhardt |

|
Introduction
When creating large Machine Learning models, we want to minimise the training time. In TensorFlow, it is possible to do mixed precision model training, which helps in significant performance improvement because it uses lower-precision operations with 16 bits (such as float16) together with single-precision operations (f.i. using float32 data type). Google TPUs and NVIDIA GPUs devices can perform operations with 16-bit datatype much faster, see Mixed precision. The improved application performance and data transfer speed result from saved memory space and the complexity of operations when using half-precision operations with float16. In this post, I will briefly outline data types and their usage with a focus on TensorFlow operations, and the main steps to perform for achieving performance gains in the mixed-precision training.
Computer Data Types
In computers, data is stored and processed in sets of bits, each of them is set to 0 (there is no signal)
or 1 (there is a signal). This is how the data is encoded to be processed through the computer circuitry.
When a byte is set to one, we have a current flow through the electronic circuit. This is called
binary data representation.
Humans are used to understanding data in more complex structures, such as the decimal number format (numbers in powers of 10).
This is why we group computer bits into sets of bytes consisting of 8 bits and further create different
computer number formats represent required number storage for other computation purposes.
The more bits we use, the more data we can store in computer memory. Please note that we have more
numerical bases, such as octal or hexadecimal, and their conversions can be easily performed, see Computer number format.
| Decimal Values | Binary Values |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
Table 1. Values in Decimal and Binary Bases
In one byte, we can store 2^8 possible values. In 4 bytes, we can store 2^32 values. We can also represent fractions using fixed-point numbers wherein we devise a defined number of bits for storing integer and fractional bits. However, this way, we cannot represent exact fractions such as 1/3, wherein the continuous tail of 3 is lost due to the limited number of bites used [1]. The range of stored values is limited by the number of bits used. We have an issue with precision loss, which is essential when running numeric computations requiring a particular precision format.
Floating-point format
To work with a more extensive range of values, we can use a floating-point numeric format when the decimal point can “float” to any position we need. We can represent fractional values to the precision necessary in our computations. Table 2 shows some possible layouts of floating-point representation for different precision levels according to the IEEE 754 standard. In short, floating-point data structures include bits for the sign, exponent, and significand parts. This representation is like the scientific notation wherein we have a significant (called the mantissa) and encode the number multiplied by the exponent. We can thus represent very large and very tiny numbers, which is quite helpful when computing neural networks.
| Precision Type | Total bits | Sign bits | Exponent bits | Significand bits | Range |
|---|---|---|---|---|---|
| Half | 16 | 1 | 5 | 10 | [-65500.0..65500.0] |
| Single | 32 | 1 | 8 | 23 | [-3.4028235e+38..3.4028235e+38] |
| Double | 64 | 1 | 11 | 52 | [-1.7976931348623157e+308..1.7976931348623157e+308] |
Table 2. Floating Point, Precision Types
I have used values such as tf.float32.min and tf.float32.max to define the ranges in Table 2. You can also check your system’s floating point information with sys.float_info
import sys
sys.float_info
sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)
The figure below shows a float number stored in two bytes of computer memory. Can you decode its value? Write me about its decimal representation or share your thoughts at the contact page.
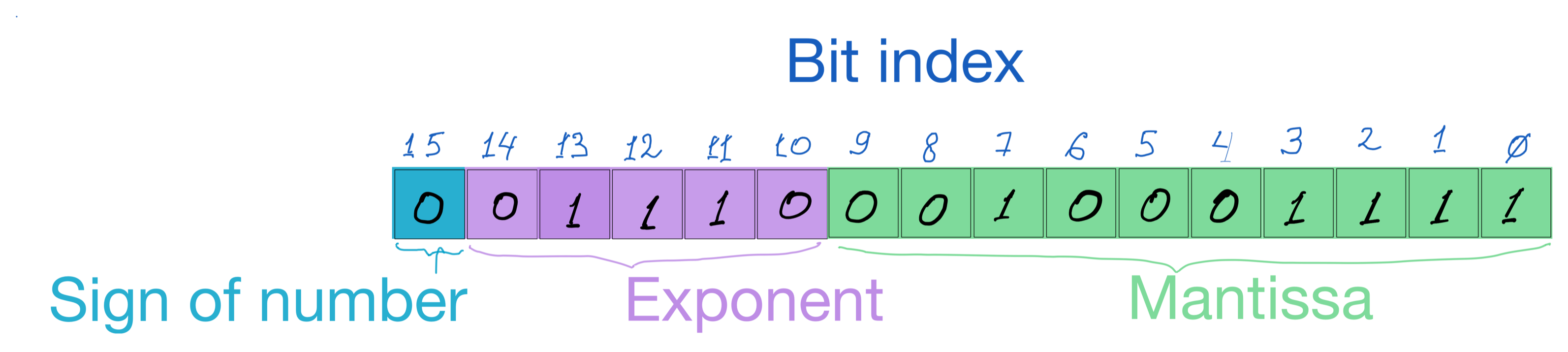
Half-precision Float-16 Representation Example
You can read about floating-point numbers and operations considering converting binary numbers to the floating-point representation at the Imperial College website.
Mixed Precision in TensorFlow
Higher precision floats occupy 32 or 64 bits of memory and thus require more computational resources for running operations. Therefore, we can use lower precision numbers f.i.float16, which can take advantage of modern accelerators designed to operate with 16-bit computations and 16-bit dtypes data much faster 5. Keras’ guide on Mixed precision explains how to combine 16-bit and 32-bit float operations for more efficient model training in TensorFlow. Next, I will describe an example of using Mixed precision following Keras guide, the TensorFlow Developer Certificate in 2022: Zero to Mastery course material, and the “Mixed precision” Colab file by TensorFlow. I will provide a working example of setting up the Mixed Precision policy and adjusting model creation steps for building fast and reliable models.
Following TensorFlow Developer Certificate in 2022: Zero to Mastery course, we implement mixed-precision TensorFlow models with the following steps:
- Activate the mixed-precision training with mixed_precision.set_global_policy(“mixed_float16”);
- Setup the output layer to use float32 data type.
Additionally, I will next show in detail how to ensure that we use the mixed-precision training, and how to check the used hardware.
GPU and TPU availability
I run the following code to check GPU and TPU availability and set the mixed-precision policy.
import TensorFlow as tf
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
policyConfig = 'mixed_bfloat16'
except ValueError:
policyConfig = 'mixed_float16'
policy = tf.keras.mixed_precision.Policy(policyConfig)
tf.keras.mixed_precision.set_global_policy(policy)
WARNING:TensorFlow:Mixed precision compatibility check (mixed_float16): WARNING Your GPU may run slowly with dtype policy mixed_float16 because it does not have compute capability of at least 7.0. Your GPU: METAL, no compute capability (probably not an Nvidia GPU) See https://developer.nvidia.com/cuda-gpus for a list of GPUs and their compute capabilities. If you will use compatible GPU(s) not attached to this host, e.g. by running a multi-worker model, you can ignore this warning. This message will only be logged once
The code output gives me a warning because my GPU (MacBook Pro M1 Max) is not designed to exploit the mixed-precision computations. Even though I do not expect performance benefits of using mixed precision on my MAC, I can still use the code to use and test the Keras API.
When using Colab, you can access the required hardware when lucky or using the Pro version. You need to ensure that your compute capability is at least 7.0. When the NVIDIA drivers are installed, we can check the GPU type:
!Nvidia-smi -L
After setting up the policy, we check which data types are used in operations and while storing variables.
print('Compute dtype: %s' % policy.compute_dtype)
print('Variable dtype: %s' % policy.variable_dtype)
Compute dtype: float16 Variable dtype: float32
Model Creation
To create our model, which should be large enough to benefit from the mixed-precision operations, we will use tf.keras.applications.EfficientNetB0. Please note that we defined the dtype=tf.float32 for our output layer.
# Download the model
baseline_model = tf.keras.applications.EfficientNetB0(include_top=False)
# Freeze underlying layers
baseline_model.trainable = False
# Create a functional model
INPUT_SHAPE = (224, 224, 3)
inputs = layers.Input(shape=INPUT_SHAPE, name="input_layer")
# For models (unlike EfficientNetBx) not including rescaling
# x = preprocessing.Rescaling(1./255)(x)
x = baseline_model(inputs, training=False)
x = layers.GlobalAveragePooling2D()(x)
x = layers.Dense(400)(x)
# Mixed precision requires output layer in float32 type, which is more numerically stabil than float16
outputs = layers.Activation("softmax", dtype=tf.float32, name="softmax_float32")(x)
# Create the model
model = tf.keras.Model(inputs, outputs)
# Compile the model
model.compile(loss="categorical_crossentropy", # sparse_categorical_crossentropy when our labels are integers
optimizer=tf.keras.optimizers.Adam(),
metrics="accuracy")
For switching off the mixed-precision policy we reset the set_global_policy for using float32 datatype again.
mixed_precision.set_global_policy("float32")
Conclusion
In this post, I have briefly outlined computer number formats with a focus on floating-point precision, which we can exploit while building mixed-precision models using modern hardware accelerators with Keras TensorFlow. A working example of the TensorFlow model using mixed-precision computing was given. I will focus on something more exciting than computer number formats in my next post!
Did you like this post? Please let me know if you have any comments or suggestions.
Posts about Machine Learning that might be interesting for youReferences
2. Computer number format, wikipedia.
5. Mixed precision, tensorflow
6. TensorFlow Developer Certificate in 2022: Zero to Mastery

|
About Elena Elena, a PhD in Computer Science, simplifies AI concepts and helps you use machine learning.
|