Introduction
What is regression? Regression defined in Wikipedia as:
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the ‘outcome’ or ‘response’ variable) and one or more independent variables (often called ‘predictors,’ ‘covariates,’ ‘explanatory variables’ or ‘features’). The most common form of regression analysis is linear regression. One finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion.
In simple words, we want to predict a numerical value based on some other numerical values, as described in the TensorFlow Developer Certificate course [1] . In Machine Learning, regression analysis is widely used for prediction and forecasting. For instance, we can use regression models to predict house sale prices. The house price can be modeled regarding the number of bedrooms, bathrooms, or garages. Other applications of regression can be to find out how many people will buy the app, to forecast seasonal sales, and even predict coordinates in an object detection task. In simple words, with regression, we want to find out answers to questions “How many?” and “How much?” [1]
Modeling Steps in TensorFlow
When we model neural networks in TensorFlow, we generally follow the steps:
- create a model and define the input, hidden and output layers, number of neurons in each layer;
- compile the model with required loss function, optimiser, evaluation metrics;
- fit the model for finding patterns between features and labels.
In the code below, we create a simple example of a regression model with input features stored in X and output
stored in y. For the demonstration purpose, I did not add much data. Instead, we use quite a small sample size to show
how we can create a regression model and further improve it while adjusting hyperparameters in the model and
compiling or fitting it.
It is also important to mention that linear regression tasks are particularly suitable for a linear trend in the dataset. Our data can be approximated by a line, as shown below. In our example, each y-value can be predicted as X+7.
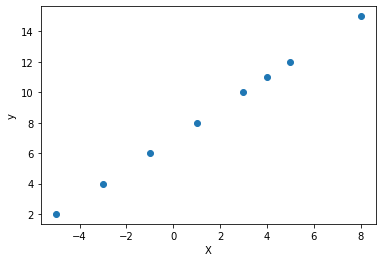
As we see, the neural network consists just of one hidden layer with one neuron, which is realising the regression functionality.
# Regression example with TensorFlow
import tensorflow as tf
# print(tf.__version__) # 2.7.0
import numpy as np
import matplotlib.pyplot as plt
# Set a random seed for reproducibility
tf.random.set_seed(57)
# Create features
X = np.array([-5., -3., -1., 1., 3., 4., 5., 8.])
# Create labels
y = np.array([2., 4., 6., 8., 10., 11., 12., 15.])
# Turn input and output Numpy arrays into tensors with float32 data type
X = tf.cast(tf.constant(X), dtype=tf.float32)
y = tf.cast(tf.constant(y), dtype=tf.float32)
# Visualise it
plt.scatter(X, y)
plt.xlabel("X")
plt.ylabel("y")
# Expand the X shape for the new version of TensorFlow
X = tf.expand_dims(X, axis=-1)
# Create a Sequential model
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile the model with Mean Absolute Error (MAE) loss function and SGD optimiser
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.SGD(),
metrics=["mae"])
# Fit the model
model.fit(X, y, epochs=5)
# Make predictions
model.predict([[10]])
Epoch 1/5 1/1 [==============================] - 0s 252ms/step - loss: 6.7141 - mae: 6.7141 Epoch 2/5 1/1 [==============================] - 0s 6ms/step - loss: 6.6816 - mae: 6.6816 Epoch 3/5 1/1 [==============================] - 0s 6ms/step - loss: 6.6491 - mae: 6.6491 Epoch 4/5 1/1 [==============================] - 0s 6ms/step - loss: 6.6166 - mae: 6.6166 Epoch 5/5 1/1 [==============================] - 0s 5ms/step - loss: 6.5841 - mae: 6.5841
We have tried to predict unseen data of [10] and observed a significant loss and MAE outputs. The predicted value was [12] instead of the [17] expected.
Improving Models
To improve our model, we can do the following in any combination, however, performing minor adjustments to see whether this takes any effect on the model performance [1]:
- adding or removing layers;
- adding the number of hidden neurons;
- changing the activation function;
- changing the optimisation function;
- adjusting the learning rate (potentially, the most critical hyperparameter);
- adding more data;
- increasing the number of epochs;
# Rebuild the model
# Create a Sequential model
model = tf.keras.Sequential([
tf.keras.layers.Dense(1)
])
# Compile the model with MAE loss function and SGD optimiser
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(lr=0.1),
metrics=["mae"])
# Fit the model
model.fit(X, y, epochs=50)
# Make predictions
model.predict([[10]])
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead. super(Adam, self).__init__(name, **kwargs) Epoch 1/50 1/1 [==============================] - 0s 261ms/step - loss: 10.2923 - mae: 10.2923 Epoch 2/50 1/1 [==============================] - 0s 9ms/step - loss: 9.9423 - mae: 9.9423 Epoch 3/50 1/1 [==============================] - 0s 7ms/step - loss: 9.5923 - mae: 9.5923 Epoch 4/50 1/1 [==============================] - 0s 5ms/step - loss: 9.2423 - mae: 9.2423 Epoch 5/50 1/1 [==============================] - 0s 5ms/step - loss: 8.8923 - mae: 8.8923 Epoch 6/50 1/1 [==============================] - 0s 5ms/step - loss: 8.5423 - mae: 8.5423 Epoch 7/50 1/1 [==============================] - 0s 8ms/step - loss: 8.2503 - mae: 8.2503 Epoch 8/50 1/1 [==============================] - 0s 5ms/step - loss: 8.0050 - mae: 8.0050 Epoch 9/50 1/1 [==============================] - 0s 6ms/step - loss: 7.7632 - mae: 7.7632 Epoch 10/50 1/1 [==============================] - 0s 5ms/step - loss: 7.5239 - mae: 7.5239 Epoch 11/50 1/1 [==============================] - 0s 5ms/step - loss: 7.2868 - mae: 7.2868 Epoch 12/50 1/1 [==============================] - 0s 6ms/step - loss: 7.0512 - mae: 7.0512 Epoch 13/50 1/1 [==============================] - 0s 5ms/step - loss: 6.8168 - mae: 6.8168 Epoch 14/50 1/1 [==============================] - 0s 6ms/step - loss: 6.5835 - mae: 6.5835 Epoch 15/50 1/1 [==============================] - 0s 4ms/step - loss: 6.3509 - mae: 6.3509 Epoch 16/50 1/1 [==============================] - 0s 7ms/step - loss: 6.1189 - mae: 6.1189 Epoch 17/50 1/1 [==============================] - 0s 8ms/step - loss: 5.8875 - mae: 5.8875 Epoch 18/50 1/1 [==============================] - 0s 6ms/step - loss: 5.6563 - mae: 5.6563 Epoch 19/50 1/1 [==============================] - 0s 8ms/step - loss: 5.4255 - mae: 5.4255 Epoch 20/50 1/1 [==============================] - 0s 7ms/step - loss: 5.1948 - mae: 5.1948 Epoch 21/50 1/1 [==============================] - 0s 5ms/step - loss: 4.9642 - mae: 4.9642 Epoch 22/50 1/1 [==============================] - 0s 11ms/step - loss: 4.7337 - mae: 4.7337 Epoch 23/50 1/1 [==============================] - 0s 7ms/step - loss: 4.5031 - mae: 4.5031 Epoch 24/50 1/1 [==============================] - 0s 11ms/step - loss: 4.2726 - mae: 4.2726 Epoch 25/50 1/1 [==============================] - 0s 7ms/step - loss: 4.0420 - mae: 4.0420 Epoch 26/50 1/1 [==============================] - 0s 6ms/step - loss: 3.8113 - mae: 3.8113 Epoch 27/50 1/1 [==============================] - 0s 10ms/step - loss: 3.5804 - mae: 3.5804 Epoch 28/50 1/1 [==============================] - 0s 9ms/step - loss: 3.4646 - mae: 3.4646 Epoch 29/50 1/1 [==============================] - 0s 5ms/step - loss: 3.4254 - mae: 3.4254 Epoch 30/50 1/1 [==============================] - 0s 4ms/step - loss: 3.3826 - mae: 3.3826 Epoch 31/50 1/1 [==============================] - 0s 5ms/step - loss: 3.3365 - mae: 3.3365 Epoch 32/50 1/1 [==============================] - 0s 8ms/step - loss: 3.3657 - mae: 3.3657 Epoch 33/50 1/1 [==============================] - 0s 7ms/step - loss: 3.3754 - mae: 3.3754 Epoch 34/50 1/1 [==============================] - 0s 7ms/step - loss: 3.3626 - mae: 3.3626 Epoch 35/50 1/1 [==============================] - 0s 9ms/step - loss: 3.3297 - mae: 3.3297 Epoch 36/50 1/1 [==============================] - 0s 6ms/step - loss: 3.2920 - mae: 3.2920 Epoch 37/50 1/1 [==============================] - 0s 10ms/step - loss: 3.2169 - mae: 3.2169 Epoch 38/50 1/1 [==============================] - 0s 9ms/step - loss: 3.1071 - mae: 3.1071 Epoch 39/50 1/1 [==============================] - 0s 9ms/step - loss: 3.0001 - mae: 3.0001 Epoch 40/50 1/1 [==============================] - 0s 5ms/step - loss: 2.8834 - mae: 2.8834 Epoch 41/50 1/1 [==============================] - 0s 8ms/step - loss: 2.7579 - mae: 2.7579 Epoch 42/50 1/1 [==============================] - 0s 6ms/step - loss: 2.6245 - mae: 2.6245 Epoch 43/50 1/1 [==============================] - 0s 8ms/step - loss: 2.5000 - mae: 2.5000 Epoch 44/50 1/1 [==============================] - 0s 7ms/step - loss: 2.4162 - mae: 2.4162 Epoch 45/50 1/1 [==============================] - 0s 7ms/step - loss: 2.3321 - mae: 2.3321 Epoch 46/50 1/1 [==============================] - 0s 6ms/step - loss: 2.2477 - mae: 2.2477 Epoch 47/50 1/1 [==============================] - 0s 4ms/step - loss: 2.1632 - mae: 2.1632 Epoch 48/50 1/1 [==============================] - 0s 6ms/step - loss: 2.0949 - mae: 2.0949 Epoch 49/50 1/1 [==============================] - 0s 7ms/step - loss: 2.0640 - mae: 2.0640 Epoch 50/50 1/1 [==============================] - 0s 6ms/step - loss: 2.0114 - mae: 2.0114 array([[17.117014]], dtype=float32)
We see pretty low loss and MAE values, and the predicted value is close to the trend. We have achieved this by employing the Adam optimiser with learning rate of 0.1 in the model compilation step and increasing the number of epochs while fitting the model.
Evaluating Models
Overall, we repeat building and fitting a model with different combinations of hyperparameters. During model training, the model learns patterns from data or finds parameters such as weights. We evaluate the model, tweak the hyperparameters and repeat its building, fitting, and evaluation steps until getting a reasonably good performance.
Overall, we require quite a large dataset to achieve a well-performing machine learning model. The more complex task is, the more data we need. We can start by generating a larger dataset for our regression example.
# Generate a larger data
X = tf.range(-100, 300, 4)
X
<tf.Tensor: shape=(100,), dtype=int32, numpy=
array([-100, -96, -92, -88, -84, -80, -76, -72, -68, -64, -60,
-56, -52, -48, -44, -40, -36, -32, -28, -24, -20, -16,
-12, -8, -4, 0, 4, 8, 12, 16, 20, 24, 28,
32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72,
76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116,
120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160,
164, 168, 172, 176, 180, 184, 188, 192, 196, 200, 204,
208, 212, 216, 220, 224, 228, 232, 236, 240, 244, 248,
252, 256, 260, 264, 268, 272, 276, 280, 284, 288, 292,
296], dtype=int32)>
# Make labels for the dataset
y = X + 7
y
<tf.Tensor: shape=(100,), dtype=int32, numpy=
array([-93, -89, -85, -81, -77, -73, -69, -65, -61, -57, -53, -49, -45,
-41, -37, -33, -29, -25, -21, -17, -13, -9, -5, -1, 3, 7,
11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59,
63, 67, 71, 75, 79, 83, 87, 91, 95, 99, 103, 107, 111,
115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163,
167, 171, 175, 179, 183, 187, 191, 195, 199, 203, 207, 211, 215,
219, 223, 227, 231, 235, 239, 243, 247, 251, 255, 259, 263, 267,
271, 275, 279, 283, 287, 291, 295, 299, 303], dtype=int32)>
Visualisation
Data visualisation helps to understand the dataset better. We can also draw training and test performance predictions against the ground truth (or labels). The model’s structure itself can be drawn with the help of TensorFlow’s plot_model functionality.
Three datasets
When we train models, we want to ensure that models not just learn the data “by heart” but can also work well with unseen data. This is called model generalisation, which can be helped by splitting our large dataset into three datasets including:
- the training dataset to train our model (70-80% of all data);
- the validation dataset to tune the model (10-15% of data available);
- test dataset to evaluate the model. (10-15% of all data).
For simplicity, we can split our dataset into training and testing sets:
# Split data into train and test sets
X_train = X[:80] # First 80% of the data
y_train = y[:80]
# Test data
X_test = X[80:] # last 20% percent of the data
y_test = y[80:]
# Visualising the data split into train an test sets
plt.figure(figsize=(10, 7))
# Plot training data in blue
plt.scatter(X_train, y_train, c="b", label="Training data")
# Plot test data in red
plt.scatter(X_test, y_test, c="r", label="Testing data")
plt.legend()
plt.xlabel("X")
plt.ylabel("y")
The figure shows the dataset with training data points in blue and testing data points in red.
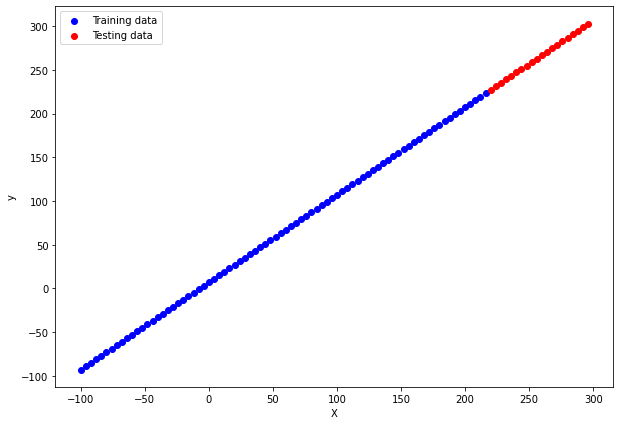
We can also perform cross-validation, which I will write in my next post.
Model predictions
Let’s create a new model and fit it with the training dataset. The neural network will contain 3 neurons in the first hidden layer and one in the output layer. We keep track of Mean Absolute Error (MAE) and Mean Squared Error (MSE) metrics while using Adam optimiser on the compile step.
# Expanding X to fit the new TensorFlow version requirement
# X = tf.expand_dims(X, axis=-1)
# Create a Sequential model
model = tf.keras.Sequential([
tf.keras.layers.Dense(3, name="first_layer"),
tf.keras.layers.Dense(1, name="output_layer")
])
# Compile the model with MAE loss function and SGD optimiser
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(lr=0.1),
metrics=["mae", "mse"])
# Fit the model
model.fit(X, y, epochs=50)
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead. super(Adam, self).__init__(name, **kwargs) Epoch 1/50 4/4 [==============================] - 0s 3ms/step - loss: 120.9953 - mae: 120.9953 - mse: 23894.6367 Epoch 2/50 4/4 [==============================] - 0s 4ms/step - loss: 37.3695 - mae: 37.3695 - mse: 2743.7510 Epoch 3/50 4/4 [==============================] - 0s 4ms/step - loss: 30.2086 - mae: 30.2086 - mse: 1857.1360 Epoch 4/50 4/4 [==============================] - 0s 3ms/step - loss: 36.0968 - mae: 36.0968 - mse: 2010.0787 Epoch 5/50 4/4 [==============================] - 0s 4ms/step - loss: 22.9426 - mae: 22.9426 - mse: 899.0366 Epoch 6/50 4/4 [==============================] - 0s 5ms/step - loss: 19.2425 - mae: 19.2425 - mse: 539.2803 Epoch 7/50 4/4 [==============================] - 0s 4ms/step - loss: 11.3198 - mae: 11.3198 - mse: 230.8450 Epoch 8/50 4/4 [==============================] - 0s 4ms/step - loss: 11.6120 - mae: 11.6120 - mse: 245.3984 Epoch 9/50 4/4 [==============================] - 0s 4ms/step - loss: 16.8810 - mae: 16.8810 - mse: 422.8721 Epoch 10/50 4/4 [==============================] - 0s 5ms/step - loss: 15.4557 - mae: 15.4557 - mse: 409.4062 Epoch 11/50 4/4 [==============================] - 0s 4ms/step - loss: 9.3804 - mae: 9.3804 - mse: 163.5114 Epoch 12/50 4/4 [==============================] - 0s 4ms/step - loss: 6.3950 - mae: 6.3950 - mse: 63.2417 Epoch 13/50 4/4 [==============================] - 0s 3ms/step - loss: 7.1727 - mae: 7.1727 - mse: 97.3974 Epoch 14/50 4/4 [==============================] - 0s 3ms/step - loss: 4.3348 - mae: 4.3348 - mse: 30.1714 Epoch 15/50 4/4 [==============================] - 0s 3ms/step - loss: 7.2365 - mae: 7.2365 - mse: 97.9294 Epoch 16/50 4/4 [==============================] - 0s 4ms/step - loss: 7.9825 - mae: 7.9825 - mse: 122.1995 Epoch 17/50 4/4 [==============================] - 0s 4ms/step - loss: 7.0333 - mae: 7.0333 - mse: 95.2871 Epoch 18/50 4/4 [==============================] - 0s 3ms/step - loss: 6.7239 - mae: 6.7239 - mse: 74.4304 Epoch 19/50 4/4 [==============================] - 0s 4ms/step - loss: 4.4470 - mae: 4.4470 - mse: 31.7933 Epoch 20/50 4/4 [==============================] - 0s 4ms/step - loss: 1.7557 - mae: 1.7557 - mse: 4.8011 Epoch 21/50 4/4 [==============================] - 0s 5ms/step - loss: 2.2091 - mae: 2.2091 - mse: 7.5242 Epoch 22/50 4/4 [==============================] - 0s 4ms/step - loss: 3.2336 - mae: 3.2336 - mse: 20.6686 Epoch 23/50 4/4 [==============================] - 0s 3ms/step - loss: 6.2744 - mae: 6.2744 - mse: 77.9671 Epoch 24/50 4/4 [==============================] - 0s 4ms/step - loss: 9.0602 - mae: 9.0602 - mse: 135.6305 Epoch 25/50 4/4 [==============================] - 0s 3ms/step - loss: 3.6392 - mae: 3.6392 - mse: 21.3788 Epoch 26/50 4/4 [==============================] - 0s 4ms/step - loss: 1.2313 - mae: 1.2313 - mse: 2.7846 Epoch 27/50 4/4 [==============================] - 0s 3ms/step - loss: 4.6018 - mae: 4.6018 - mse: 35.7042 Epoch 28/50 4/4 [==============================] - 0s 3ms/step - loss: 5.4567 - mae: 5.4567 - mse: 53.5563 Epoch 29/50 4/4 [==============================] - 0s 4ms/step - loss: 3.9640 - mae: 3.9640 - mse: 33.2863 Epoch 30/50 4/4 [==============================] - 0s 3ms/step - loss: 2.6091 - mae: 2.6091 - mse: 13.5995 Epoch 31/50 4/4 [==============================] - 0s 5ms/step - loss: 7.2700 - mae: 7.2700 - mse: 86.4028 Epoch 32/50 4/4 [==============================] - 0s 3ms/step - loss: 10.4771 - mae: 10.4771 - mse: 171.6588 Epoch 33/50 4/4 [==============================] - 0s 3ms/step - loss: 8.3980 - mae: 8.3980 - mse: 161.0003 Epoch 34/50 4/4 [==============================] - 0s 4ms/step - loss: 4.2892 - mae: 4.2892 - mse: 43.4268 Epoch 35/50 4/4 [==============================] - 0s 3ms/step - loss: 1.9115 - mae: 1.9115 - mse: 8.9037 Epoch 36/50 4/4 [==============================] - 0s 3ms/step - loss: 5.1150 - mae: 5.1150 - mse: 46.9002 Epoch 37/50 4/4 [==============================] - 0s 4ms/step - loss: 6.2562 - mae: 6.2562 - mse: 74.0645 Epoch 38/50 4/4 [==============================] - 0s 3ms/step - loss: 3.2418 - mae: 3.2418 - mse: 17.0526 Epoch 39/50 4/4 [==============================] - 0s 5ms/step - loss: 3.0819 - mae: 3.0819 - mse: 18.1384 Epoch 40/50 4/4 [==============================] - 0s 4ms/step - loss: 2.2617 - mae: 2.2617 - mse: 9.4483 Epoch 41/50 4/4 [==============================] - 0s 3ms/step - loss: 4.8202 - mae: 4.8202 - mse: 47.1045 Epoch 42/50 4/4 [==============================] - 0s 4ms/step - loss: 7.5390 - mae: 7.5390 - mse: 125.5217 Epoch 43/50 4/4 [==============================] - 0s 3ms/step - loss: 4.8652 - mae: 4.8652 - mse: 39.2499 Epoch 44/50 4/4 [==============================] - 0s 4ms/step - loss: 4.8499 - mae: 4.8499 - mse: 42.2790 Epoch 45/50 4/4 [==============================] - 0s 4ms/step - loss: 1.0383 - mae: 1.0383 - mse: 3.7415 Epoch 46/50 4/4 [==============================] - 0s 3ms/step - loss: 0.8587 - mae: 0.8587 - mse: 1.4711 Epoch 47/50 4/4 [==============================] - 0s 4ms/step - loss: 1.6601 - mae: 1.6601 - mse: 6.1024 Epoch 48/50 4/4 [==============================] - 0s 3ms/step - loss: 3.7125 - mae: 3.7125 - mse: 30.4232 Epoch 49/50 4/4 [==============================] - 0s 6ms/step - loss: 5.7093 - mae: 5.7093 - mse: 60.4152 Epoch 50/50 4/4 [==============================] - 0s 4ms/step - loss: 5.1068 - mae: 5.1068 - mse: 39.9806
We use plot_model() method to draw the network shown below.
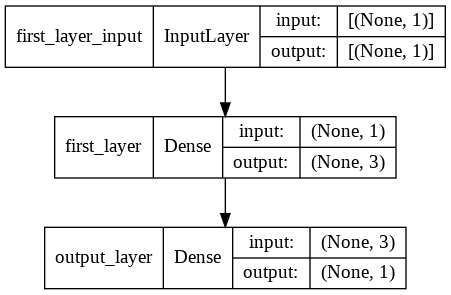
# Import plot_model
from tensorflow.keras.utils import plot_model
plot_model(model, show_shapes=True)
It is helpful to explore how far the model predictions are from the ground truth. We visualise the model predictions against the ground truth in a scatter plot.
# Make some predictions
y_pred = model.predict(X_test)
# Print the predicted and ground truth values
for predicted, truth in zip(y_pred, y_test):
print("Ground truth:%d predicted:%f"%(truth.numpy(), predicted[0]))
Ground truth:227 predicted:217.726746 Ground truth:231 predicted:221.557556 Ground truth:235 predicted:225.388351 Ground truth:239 predicted:229.219147 Ground truth:243 predicted:233.049957 Ground truth:247 predicted:236.880753 Ground truth:251 predicted:240.711548 Ground truth:255 predicted:244.542343 Ground truth:259 predicted:248.373154 Ground truth:263 predicted:252.203949 Ground truth:267 predicted:256.034760 Ground truth:271 predicted:259.865570 Ground truth:275 predicted:263.696350 Ground truth:279 predicted:267.527161 Ground truth:283 predicted:271.357971 Ground truth:287 predicted:275.188782 Ground truth:291 predicted:279.019562 Ground truth:295 predicted:282.850372 Ground truth:299 predicted:286.681152 Ground truth:303 predicted:290.511963
Finally, we create a data plotting function to draw scatter plots of training, testing and predicted datasets.
# A plotting function
def plot_data(train_data=X_train, train_labels=y_train,
test_data=X_test, test_labels=y_test, predictions=y_pred):
plt.figure(figsize=(10, 5))
# Drawing scatter plots
plt.scatter(train_data, train_labels, c="g", label="Training data")
plt.scatter(test_data, test_labels, c="b", label="Testing data")
plt.scatter(test_data, predictions, c="r", label="Predictions data")
plt.legend()
plot_data()
The predicted data is below the testing data values, as we see from the plot.
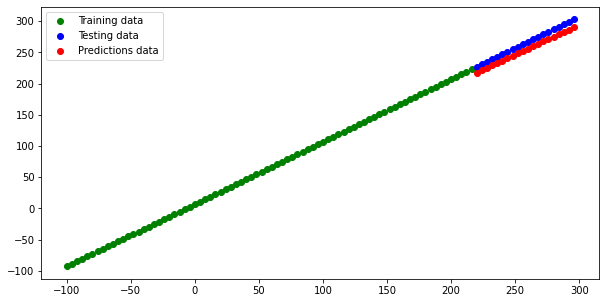
Evaluating the Model Predictions
We use the models’ evaluation method with the testing dataset to evaluate the model predictions. Since we defined the MAE and MSE metrics during the compilation step, we get these values in the result.
# Evaluate the model on the test set
model.evaluate(X_test, y_test)
1/1 [==============================] - 0s 125ms/step - loss: 10.4243 - mae: 10.4243 - mse: 109.5560 [10.424253463745117, 10.424253463745117, 109.55604553222656]
We can also calculate the MAE and MSE having predicted (y_pred) and ground truth labels (y_test).
# Calculate the Mean Absolute Error (MAE) with y_pred and y_test
# Please note that we remove an extra dimension with tf.squeeze
mae = tf.metrics.mean_absolute_error(y_true=y_test, y_pred=tf.squeeze(y_pred))
# Calculate the Mean Square Error (MSE)
mse = tf.metrics.mean_squared_error(y_true=y_test, y_pred=tf.squeeze(y_pred))
print("MAE=%f, MSE=%f"%(mae, mse))
MAE=10.415435, MSE=109.370789
Did you like this post? Please let me know if you have any comments or suggestions.
Python posts that might be interesting for youConclusion
In this post, I have described regression modeling in TensorFlow. We have predicted a numerical value and adjusted hyperparameters to better model performance with a simple neural network. We generated a dataset, demonstrated a simple data split into training and testing sets, visualised our data and the created neural network, evaluated our model using a testing dataset. In my next post, I will go more into the model evaluation and so much used cross-validation technique.
For writing this post, I have used TensorFlow documentation and tutorials at Udemy, TensorFlow Developer Certificate in 2022: Zero to Mastery.

