TensorFlow: Evaluating the Regression Model25 Jan 2022 / 9 minutes to read Elena Daehnhardt |

|
Introduction
In the previous post, we have created several simple regression models with TensorFlow’s Sequential model. Herein we continue more in-depth about model evaluation using the testing dataset.
Data Preparation
First of all, to ensure the reproducibility of results, we set a random seed (please check my previous post if you are curious about seeds in TensorFlow). As in the previous post on regression in TensorFlow, we use tf.range() function for generating a set of X input values, and also y outputs as follows:
# Creating a random seed
tf.random.set_seed(57)
# Generating data
X = tf.range(-100, 300, 4)
y = X + 7
X, y
(<tf.Tensor: shape=(100,), dtype=int32, numpy=
array([-100, -96, -92, -88, -84, -80, -76, -72, -68, -64, -60,
-56, -52, -48, -44, -40, -36, -32, -28, -24, -20, -16,
-12, -8, -4, 0, 4, 8, 12, 16, 20, 24, 28,
32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72,
76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116,
120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160,
164, 168, 172, 176, 180, 184, 188, 192, 196, 200, 204,
208, 212, 216, 220, 224, 228, 232, 236, 240, 244, 248,
252, 256, 260, 264, 268, 272, 276, 280, 284, 288, 292,
296], dtype=int32)>, <tf.Tensor: shape=(100,), dtype=int32, numpy=
array([-93, -89, -85, -81, -77, -73, -69, -65, -61, -57, -53, -49, -45,
-41, -37, -33, -29, -25, -21, -17, -13, -9, -5, -1, 3, 7,
11, 15, 19, 23, 27, 31, 35, 39, 43, 47, 51, 55, 59,
63, 67, 71, 75, 79, 83, 87, 91, 95, 99, 103, 107, 111,
115, 119, 123, 127, 131, 135, 139, 143, 147, 151, 155, 159, 163,
167, 171, 175, 179, 183, 187, 191, 195, 199, 203, 207, 211, 215,
219, 223, 227, 231, 235, 239, 243, 247, 251, 255, 259, 263, 267,
271, 275, 279, 283, 287, 291, 295, 299, 303], dtype=int32)>)
We want to separate training and testing datasets for the respective model training and evaluation steps, using split_data() function:
# Split data into train and test sets
def split_data(X, y):
X_train = X[:80] # First 80% of the data
y_train = y[:80]
X_test = X[80:] # last 20% percent of the data
y_test = y[80:]
return(X_train, X_test, y_train, y_test)
(X_train, X_test, y_train, y_test) = split_data(X, y)
X_train = tf.expand_dims(X_train, axis = -1)
X_test = tf.expand_dims(X_test, axis = -1)
Calculating Error Metrics
Using the ground-truth y_pred and testing data y_test, we calculate Means Absolute Error (MAE) and Mean Squared Error (MSE) while considering that MSE emphasises the significant outliers in the data. The MAE and MSE are usual metrics to go for in the regression problems. You can also employ Huber metric available in TensorFlow.
# Calculate MAE and MSE
def get_errors(y_test, y_pred):
# we remove an extra dimension with tf.squeeze
y_pred = tf.squeeze(y_pred)
# Calculate the Mean Absolute Error (MAE)
mae = tf.metrics.mean_absolute_error(y_true=y_test, y_pred=y_pred).numpy()
# Calculate the Mean Square Error (MSE)
mse = tf.metrics.mean_squared_error(y_true=y_test, y_pred=y_pred).numpy()
# print("MAE=%f, MSE=%f"%(mae, mse))
return (mae, mse)
Creating Models
In experimentation, we create, compile, fit and evaluate several models with defined hyperparameters and evaluation metrics for finding a well-performing model. We will follow the same steps while creating different experimental models. We changed the hyperparameters to find out their best combination for a lower error rate. Thus, we create a function create_model(), which will take in the main hyperparameters, including the number of neurons in the first dense layer (model creation), and the learning rate of the Adam optimiser (model compilation step). The function returns compiled model, which is yet to be trained (or fitted).
# Create and compile a model with defined neurons and learning rate
def create_model(neurons_number=3, learning_rate=0.1):
# Create a model with 6 neurons in the first layer
model = tf.keras.Sequential([
tf.keras.layers.Dense(neurons_number),
tf.keras.layers.Dense(1)])
# Compile the model
model.compile(loss=tf.keras.losses.mae,
optimizer=tf.keras.optimizers.Adam(lr=learning_rate),
metrics=["mae", "mse"])
return model
# We will evaluate four possible hyperparameter sets defined:
neurons = [3, 6, 3, 6];
epochs = [50, 100, 50, 100]
learning_rates = [0.1, 0.001, 0.001, 0.1]
Evaluating Models
With the prepared dataset, the defined hyperparameter sets that we want to test, model creation function, we focus on experimenting with different models. We cycle over the hyperparameter sets and call the create_model() function to create Sequential models with each parameter combination.
# We will store the evaluation results in the array
evaluation_results=[]
# We zeep the hyperparameters to create four Sequencial models to create, fit and analyse
for neurons, epoch, rate in zip(neurons, epochs, learning_rates):
# Create and fit the model
model = create_model(neurons_number=neurons, learning_rate=rate)
model.fit(X_train, y_train, epochs=epoch, verbose=0)
# Predict the test set
y_pred = model.predict(X_test)
# Store results
mae, mse = get_errors(y_test, y_pred)
evaluation_results.append({"neurons": neurons, "learning_rate": rate,
"epochs": epoch, "mae": mae, "mse": mse})
# Show evaluation results in a Pandas DataFrame
import pandas as pd
pd.DataFrame(evaluation_results)
The table below shows that the Sequential model with 3 neurons and Adam optimiser with a learning rate of 0.1 has the lowest MAE and MSE values compared with the 3 other models.
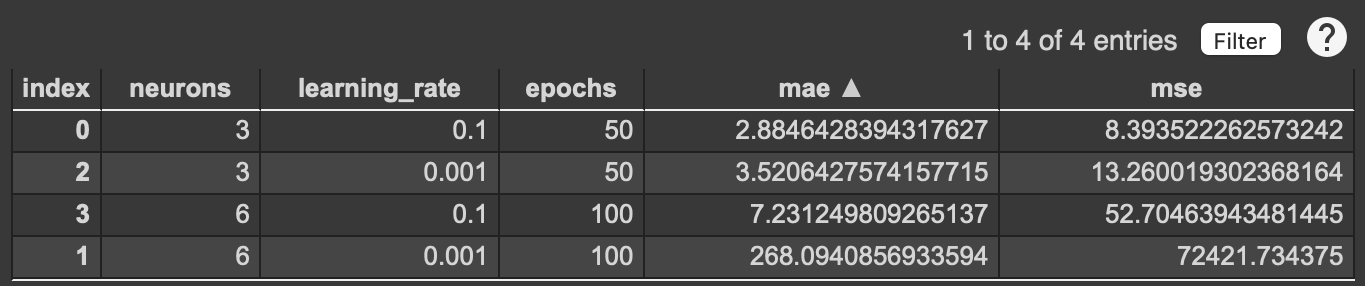
Conclusion
In this post, we have performed the evaluation of four regression models using TensorFlow. MAE and MSE error metrics were used to compare the Sequential models while finding the best neural network architecture regarding the defined hyperparameters.
Did you like this post? Please let me know if you have any comments or suggestions.
Python posts that might be interesting for youThanks

|
About Elena Elena, a PhD in Computer Science, simplifies AI concepts and helps you use machine learning.
|