Introduction
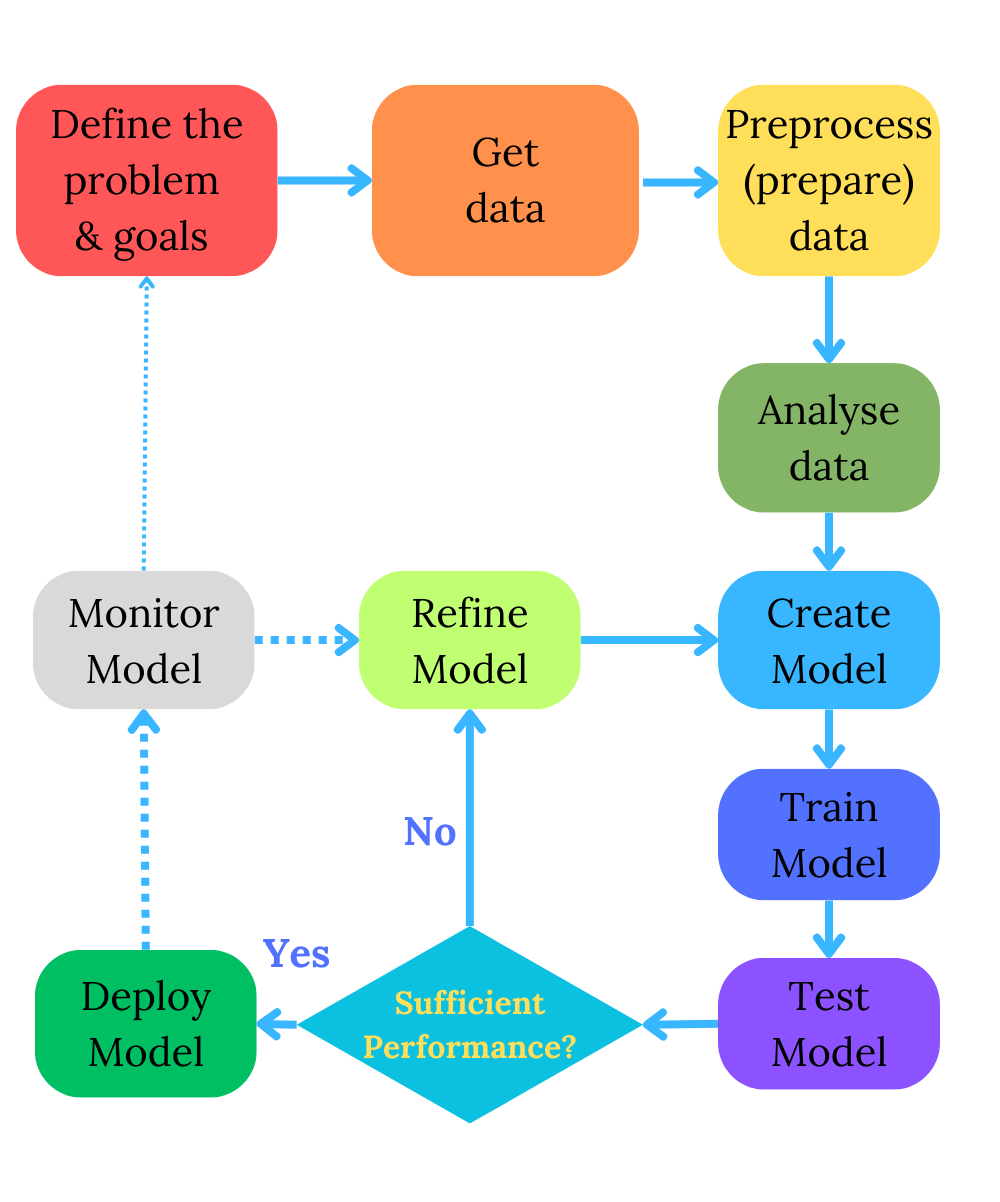
In machine learning, we usually start from a simple baseline model and progressively adjust its complexity until we reach that spot with the best model performance. We play with the model to fine-tune its parameters and complexity in an iterative process described in my previous post, the Machine Learning Process, wherein I have posted this diagram.
We want our Machine Learning (ML) model to solve a particular problem, for instance, detecting spam in e-mail messages.
The model should be well-trained, however, generalisable to new data when new spam messages not existing in the training dataset are received. In short, the model has to be well-fitted.
ML models should be resilient to noisy data, work well on unseen data, and help make unbiased decisions. We want to achieve an optimal variance to make generalisable models work well with new data.
How can we do this? Let’s detail the most essential machine learning concepts, particularly, the bias-variance challenge.
Important concepts
Different machine learning algorithms seek to minimise the chosen loss function during training. The algorithm aims to find the model parameters (coefficients or weights) that minimise the error on the training data. Minimising this error helps ensure the model generalises well to unseen data and makes accurate predictions or classifications.
In general, algorithmic error is typically decomposed into three fundamental components (see Bias and Variance TradeOff):
- Bias squared (Bias^2)
- Variance (Variance)
- Irreducible error
Error = Bias^2 + Variance + Irreducible Error
Irreducible error, also known as irreducible uncertainty or irreducible noise, is a component of the total error in a predictive model that cannot be reduced or eliminated by improving the model itself. It represents the inherent unpredictability and randomness in the data or the underlying process being modelled. This error source is considered “irreducible” because it is beyond the control of the model, and no matter how complex or sophisticated the model is, it cannot account for or reduce this source of error.
Irreducible error arises from various factors, including:
-
Inherent Data Variability: Data collected from the real world often contains inherent noise and randomness. Even with a perfect model, there will always be a level of unpredictability in the data.
-
Measurement Error: Data may be subject to measurement errors, inaccuracies, or imprecisions, which introduce noise and contribute to the irreducible error.
-
Unaccounted Variables: There may be unobserved or unmeasured variables that influence the outcome but are not included in the model, leading to unpredictability.
-
Random Events: Some processes, particularly in fields like finance or complex natural systems, are influenced by random events that cannot be modelled or predicted accurately.
The presence of irreducible error is an essential concept in statistics and machine learning. It emphasises that there is a limit to how well a model can perform, as some level of error will always be present due to the intrinsic unpredictability in the data.
Modellers must focus on reducing bias and variance (the reducible components of error) while acknowledging and accepting the existence of irreducible errors in their predictions and analyses.
Let’s define bias and variance concepts.
Bias
Bias in machine learning refers to systematic and unfair discrimination or inaccuracies in the predictions and decisions made by a machine learning model.
It can occur at various stages of the machine learning process, from data collection and preprocessing to model training and deployment. Bias can manifest in several ways:
-
Data Bias occurs when the training data used to build a machine-learning model does not represent the real-world population it serves. Data bias can result from underrepresented or overrepresented groups in the training data, leading to unfair predictions for specific groups.
-
Algorithmic Bias occurs when machine learning algorithms inherently favour certain groups or types of data due to their design. For example, if an algorithm is designed with features that favour one group over another, it can introduce bias.
-
Labeling Bias surfaces when inaccurate labels in the training data can lead to biased models. For example, if human labellers are biased in their annotations, the model will learn and perpetuate those biases.
-
Feedback Loop Bias happens when machine learning models are used in real-world applications; their predictions can influence future data collection and decision-making. If the initial predictions were biased, this feedback loop can amplify and perpetuate bias over time.
-
Deployment Bias emerges when models are deployed in real-world applications, as they may interact with biased systems or human decision-makers. For instance, a biased model used in a hiring process can lead to discriminatory hiring decisions.
Bias in machine learning can have significant ethical, social, and legal implications, as it can lead to unfair treatment or discrimination and perpetuate existing societal biases.
Addressing bias in machine learning involves careful data collection, preprocessing, algorithm design, and ongoing model performance monitoring. It often requires a combination of technical solutions, ethical considerations, and regulatory frameworks to ensure that machine learning systems make fair and unbiased predictions.
The squared bias measures how far, on average, the model’s predictions are from the actual values.
Bias^2 = E[(f̂(x) - f(x))^2]
Where:
- E denotes the expectation or average.
- f̂(x) is the predicted value or output of the model for a given input x.
- f(x) is the true or target value for the same input x.
Variance
Variance in machine learning refers to the sensitivity of a machine learning model to the fluctuations or noise in the training data. It represents the degree to which the model’s predictions vary when different training datasets are used.
In other words, variance quantifies how well a model generalises to new, unseen data and whether it overfits or underfits the training data.
Here’s a more detailed explanation of variance and its relationship with model performance:
-
High Variance (Overfitting): A model with high variance is overly complex and fits the training data very closely, capturing not only the underlying patterns but also the noise or randomness in the data. As a result, it performs well on the training data but poorly on new, unseen data because it has essentially memorised the training data rather than learned the underlying relationships. Overfit models often need to be more flexible and exhibit high variance.
-
Low Variance (Underfitting): A model with low variance needs to be more complex and capture the underlying patterns in the training data. It performs poorly on the training and new, unseen data because it fails to generalise. Underfit models are often too rigid and exhibit low variance.
-
Optimal Variance (Generalisation): Machine learning aims to find a balance between high and low variance, where the model can generalise well to new data while still capturing the essential patterns in the training data. This balance results in a model that provides accurate predictions on unseen data, which is the primary objective of machine learning experimentation.
Variance in machine learning is a critical concept related to the model’s ability to generalise from the training data to new, unseen data. Achieving the right bias-variance balance is essential for building models that make accurate predictions and avoid overfitting or underfitting.
The variance measures how much the predictions for a given input vary across different training sets.
Variance = E[(f̂(x) - E[f̂(x)])^2]
Where:
- E denotes the expectation or average.
- f̂(x) is the predicted value or output of the model for a given input x.
- E[f̂(x)] is the expected value of the predictions across different training sets for the same input x.
Bias–variance challenge
I suggest you read Wikipedia’s Bias–variance tradeoff on this topic.
If you’re eager to delve deeper into the bias-variance tradeoff, Scott Fortmann-Roe’s classic paper, Understanding the Bias-Variance Tradeoff, is a must-read. There are also some maths. I am sure you will love it since you are reading this blog. However, I like to keep things simple and preserve the whole story from the application point of view. Keep reading.
“A picture is worth a thousand words. Below, you see the essence of the bias-variance dilemma in which we seek to find the lowest bias and variance point when creating machine-learning models.”
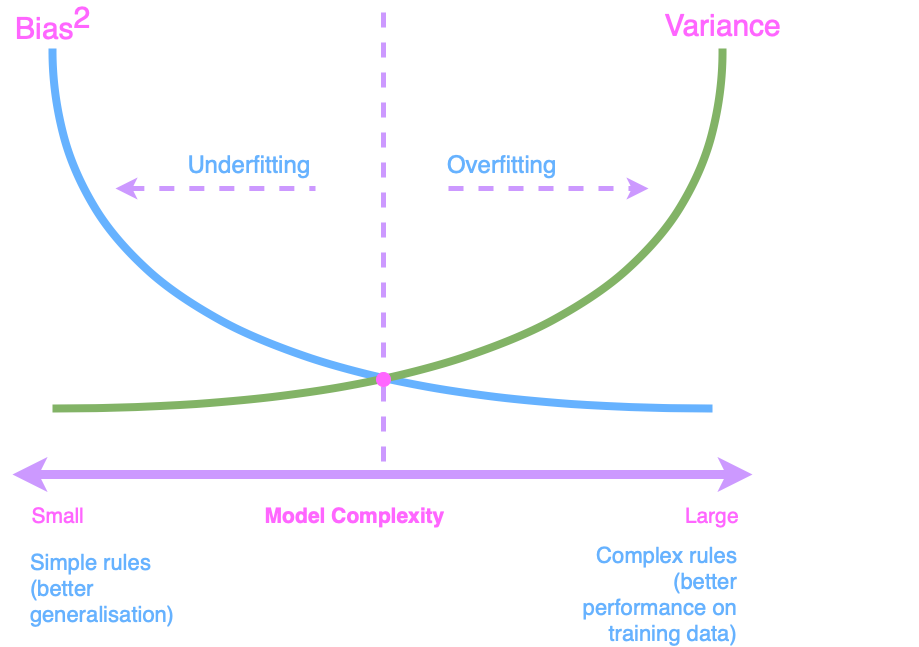
Fitting models
Feeding the models with the training data is called “fitting models”. There are certain situations when models are not trained well.
Underfitting is a situation in machine learning where a model is too simple to capture the underlying patterns in the data. It occurs when the model is not complex enough to fit the training data effectively. As a result, the model needs to perform better on the training data and unseen or test data. Underfit models often have high bias, making oversimplified assumptions about the data, leading to inaccurate predictions. In essence, underfitting means the model is “too weak” to represent the data, and it fails to generalise well.
Overfitting is a common issue in machine learning, where a model is excessively complex, effectively “memorising” the training data rather than learning the underlying patterns. This results in a model that performs very well on the training data but poorly on unseen or test data. Overfit models have high variance, meaning they capture noise and irrelevant details in the training data, which do not generalise to new data.
In overfitting, the model becomes overly sensitive to the noise in the training data, making it less capable of making accurate predictions on data it has yet to see. It fails to generalise well, leading to poor performance in real-world applications. Techniques like cross-validation, regularisation, and feature selection can be applied to mitigate overfitting to create more robust and generalisable machine learning models.
The Baseline Model
The “baseline model” is intentionally kept simple, starting as an underfit model with high bias. High bias implies that the model oversimplifies the data, potentially missing crucial patterns. A high bias we further improve by increasing the model complexity. It is crucial to stop when the model has a reasonable variance.
Increasing model complexity
Increasing model complexity is a common approach in machine learning when you want to capture more intricate patterns in your data. However, it should be done carefully, as overly complex models may lead to overfitting. Here are several ways to increase model complexity:
-
Add More Features: Include additional relevant features or input variables that may contain useful information for your problem. More features can provide the model with more information to learn from.
-
Use Complex Algorithms: Choose more complex machine learning algorithms, such as deep neural networks, ensemble methods (e.g., random forests, gradient boosting), or models with more parameters. These algorithms can handle complex relationships in the data.
-
Increase Model Depth: If you’re using neural networks, increase the number of layers and neurons in the network. Deeper networks can capture intricate hierarchical patterns in the data.
-
Adjust Hyperparameters: Fine-tune hyperparameters, such as learning rates, regularisation strengths, or the number of decision trees in an ensemble. Optimising hyperparameters can help the model find the right balance between complexity and generalisation.
-
Use Nonlinear Activation Functions: If you’re working with neural networks, use nonlinear activation functions like ReLU (Rectified Linear Unit) or sigmoid to introduce nonlinearity into the model, allowing it to learn more complex functions.
-
Increase Training Data: If possible, obtain a larger dataset. More data can help a model generalise better, even when it’s more complex. However, collecting additional data is only sometimes feasible.
-
Regularization: Use techniques like L1 or L2 regularization to control model complexity. Regularisation penalizes large coefficients in the model, preventing it from becoming too complex.
-
Feature Engineering: Create more sophisticated features by combining existing ones, engineering interactions between features, or applying domain-specific transformations.
-
Consider Advanced Architectures: Explore advanced model architectures, such as convolutional neural networks (CNNs) for image data, recurrent neural networks (RNNs) for sequential data, or transformers for natural language processing tasks.
-
Ensemble Models: Combine multiple models, which can be simpler models or models of varying complexity, to create a more complex ensemble model. Techniques like bagging and boosting can be beneficial.
Remember that increasing model complexity comes with a trade-off. While it can help the model fit the training data better, it may also make it more prone to overfitting, where it performs poorly on unseen data. It’s essential to monitor the model’s performance on a validation set and use techniques like cross-validation to strike the right balance between complexity and generalisation.
Balancing the bias and variance
Thus, we balance the bias and variance to perform well on the test data. We remember that too large or complex models might memorise our training dataset and become irrelevant to the test data.
To enhance its performance, we progressively increase the model’s complexity. The challenge lies in knowing when to stop. We aim for a sweet spot where the model exhibits reasonable bias and variance.
In summary:
High bias is analogous to underestimating the data, leading to oversimplification.
High variance is akin to overreacting to the data, memorising it, and struggling to generalise.
Striking the Right Balance
The pivotal question arises: How do we pinpoint when our model’s complexity is “just right”? Techniques like cross-validation, regularisation, and feature selection can be employed to manage variance and achieve better model performance.
Cross-validation helps evaluate the model’s performance on different subsets of the training data, giving insights into its generalisation abilities.
One of my next posts is about Cross-Validation techniques. I suggest subscribing to get the notification sent to your e-mail box.
To keep it simple, Cross-Validation is about repeatedly breaking a dataset into training and test parts that the model repeatedly tested on “unseen data”.
Regularisation techniques, such as L1 and L2 regularisation, can control the complexity of the model, preventing it from overfitting.
Feature selection allows you to choose the most relevant features, which can reduce variance by removing noise from the data.
Python code
Let’s move from theory to practice with Python. The versatile scikit-learn library offers powerful tools for understanding the bias-variance tradeoff.
In my previous post Machine Learning Process, we defined the main steps in ML experiments, and we had a practical example of using scikit-learn library while comparing Decision Trees and Random Forest models in Decision Tree versus Random Forest, and Hyperparameter Optimisation.
On this blog, you can find the data preprocessing and preparation with the Titanic dataset in Machine Learning Tests using Titanic dataset. There are also installation instructions should you need to install the libraries we next use.
In short, we have preprocessed the Titanic dataset and created simple, but very efficient, supervised ML models, including the Decision Tree and Random Forest.
Herein, we will perform cross-validation to find out about the bias and variance of these models.
Creating models
In my previous post Decision Tree versus Random Forest, and Hyperparameter Optimisation, we created the Decision Tree and Random Forest models.
You can get the code for both models’ creation in the Colab notebook. It also includes the code below for getting the bias and variance of these models.
We will use the decision tree as our baseline model, further compared with the random forest model.
Random Forest is an ensemble of multiple decision trees that work in parallel. It has a higher complexity.
We will aim to lower bias and variance. Will it work out well? Let’s see.
Find the models’ bias and variance
To calculate the bias and variance of a machine learning model, you typically need to use techniques such as cross-validation. Here’s a Python code example that demonstrates how to calculate the bias and variance of a model using scikit-learn and the sklearn.model_selection.cross_val_score function:
We use cross-validation to estimate bias and variance. The cross_val_score function performs k-fold cross-validation (in this case, with cv=5) and calculates the negative mean squared error for each fold. We negate this value to obtain the mean squared error. The negative mean squared error represents the bias for each fold. We then calculate the mean and standard deviation of these bias scores to estimate the overall bias and variance of the model.
We use 5-fold cross-validation to estimate the mean squared error for each fold, which helps us estimate bias and variance.
# Import cross_val_score
from sklearn.model_selection import cross_val_score
# Calculate the Decision Tree model's bias using cross-validation
bias_scores = cross_val_score(decision_tree_clf, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
bias = -bias_scores.mean()
# Calculate variance using cross-validation
variance = bias_scores.std()
print(f'Bias: {bias}')
print(f'Variance: {variance}')
Bias: 0.24998522604156403 Variance: 0.02736821291803949
# Calculate the Random Forest model's bias using cross-validation
bias_scores = cross_val_score(random_forest_clf, X_train, y_train, cv=5, scoring='neg_mean_squared_error')
bias = -bias_scores.mean()
# Calculate variance using cross-validation
variance = bias_scores.std()
print(f'Bias: {bias}')
print(f'Variance: {variance}')
Bias: 0.19808923470895298 Variance: 0.018009815555289254
Combining multiple trees, achieved through row and column sampling, results in a Random Forest model offering lower bias and variance than the baseline Decision Tree model.
For more on bias and variance using Python, refer to the official scikit-learn guide at Underfitting vs. Overfitting.
That’s all! Let’s summarise once again:
High bias is practically ignoring the data
High variance is learning data by “heart”
In this post, we compared just two models. In practice, we will create many more models :)
Now, we know how to apply cross-validation, which can help reach this sweet point of finding an appropriate balance between bias and variance!
Conclusion
As you continue your journey in the dynamic world of machine learning, remember that understanding the bias-variance tradeoff is a fundamental skill. Whether you’re a beginner or an expert, finding that “just right” model is crucial—a model that performs optimally on training and test data.
Did you like this post? Please let me know if you have any comments or suggestions.
Posts about Machine Learning that might be interesting for youReferences
1. All the code in the Colab notebook
3. Decision Tree versus Random Forest, and Hyperparameter Optimisation
6. Understanding the Bias-Variance Tradeoff
7. Underfitting vs. Overfitting¶
8. The Titanic dataset from Kaggle
9. Python tutorials repository

|
About Elena Elena, a PhD in Computer Science, simplifies AI concepts and helps you use machine learning.
|
