TensorFlow: Multiclass Classification Model06 Feb 2022 / 34 minutes to read Elena Daehnhardt |

|
Introduction
In Machine Learning, the classification problem is categorising input data into different classes. For instance, we can categorise email messages into two groups: spam or not spam. In this case, we have two classes, we talk about binary classification. When we have more than two classes, we talk about multiclass classification. In this post, I am going to address the latest multiclass classification, on the example of categorising clothing items into clothing types based on the Fashion MNIST dataset. The code and general concepts are adopted from TensorFlow Developer Certificate in 2022: Zero to Mastery. Herein I will give a concise summary of what I have learned, in simple words as usual.
Loading Dataset
The Zalando fashion dataset is available in the keras datasets module. With the following code, we download the dataset into training and testing datasets, and create human-readable labels.
First of all, we need to import all required libraries.
import tensorflow as tf
import pandas as pd
import numpy as np
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import confusion_matrix
import itertools
import random
import matplotlib.pyplot as plt
Next, we load the Fashion MNIST dataset from keras.
# Fashion dataset
fashion_mnist = tf.keras.datasets.fashion_mnist
# Get the training and testing data
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# Create human-readable labels
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-labels-idx1-ubyte.gz 32768/29515 [=================================] - 0s 0us/step 40960/29515 [=========================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/train-images-idx3-ubyte.gz 26427392/26421880 [==============================] - 0s 0us/step 26435584/26421880 [==============================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-labels-idx1-ubyte.gz 16384/5148 [===============================================================================================] - 0s 0us/step Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/t10k-images-idx3-ubyte.gz 4423680/4422102 [==============================] - 0s 0us/step 4431872/4422102 [==============================] - 0s 0us/step
We see the shapes of downloaded training and testing datasets with their labels.
print(f"Train images shape: {train_images.shape}")
print(f"Test images shape: {test_images.shape}")
print(f"Train labels shape: {train_labels.shape}")
print(f"Test labels shape: {test_labels.shape}")
Train images shape: (60000, 28, 28) Test images shape: (10000, 28, 28) Train labels shape: (60000,) Test labels shape: (10000,)
Data Exploration
We observe that the dataset consists of numerical data organised into a set of 28x28 matrices with values from 0 to 255, consisting of NumPy arrays of grayscale image data. As we see from the first data row, its shape is (28, 28), the maximum value is 255.
train_images[0].shape, train_images[0].min(), train_images[0].max()
((28, 28), 0, 255)
train_images[0]
array([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1,
0, 0, 13, 73, 0, 0, 1, 4, 0, 0, 0, 0, 1,
1, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 3,
0, 36, 136, 127, 62, 54, 0, 0, 0, 1, 3, 4, 0,
0, 3],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6,
0, 102, 204, 176, 134, 144, 123, 23, 0, 0, 0, 0, 12,
10, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 155, 236, 207, 178, 107, 156, 161, 109, 64, 23, 77, 130,
72, 15],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
69, 207, 223, 218, 216, 216, 163, 127, 121, 122, 146, 141, 88,
172, 66],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0,
200, 232, 232, 233, 229, 223, 223, 215, 213, 164, 127, 123, 196,
229, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
183, 225, 216, 223, 228, 235, 227, 224, 222, 224, 221, 223, 245,
173, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
193, 228, 218, 213, 198, 180, 212, 210, 211, 213, 223, 220, 243,
202, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 3, 0, 12,
219, 220, 212, 218, 192, 169, 227, 208, 218, 224, 212, 226, 197,
209, 52],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 0, 99,
244, 222, 220, 218, 203, 198, 221, 215, 213, 222, 220, 245, 119,
167, 56],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 0, 0, 55,
236, 228, 230, 228, 240, 232, 213, 218, 223, 234, 217, 217, 209,
92, 0],
[ 0, 0, 1, 4, 6, 7, 2, 0, 0, 0, 0, 0, 237,
226, 217, 223, 222, 219, 222, 221, 216, 223, 229, 215, 218, 255,
77, 0],
[ 0, 3, 0, 0, 0, 0, 0, 0, 0, 62, 145, 204, 228,
207, 213, 221, 218, 208, 211, 218, 224, 223, 219, 215, 224, 244,
159, 0],
[ 0, 0, 0, 0, 18, 44, 82, 107, 189, 228, 220, 222, 217,
226, 200, 205, 211, 230, 224, 234, 176, 188, 250, 248, 233, 238,
215, 0],
[ 0, 57, 187, 208, 224, 221, 224, 208, 204, 214, 208, 209, 200,
159, 245, 193, 206, 223, 255, 255, 221, 234, 221, 211, 220, 232,
246, 0],
[ 3, 202, 228, 224, 221, 211, 211, 214, 205, 205, 205, 220, 240,
80, 150, 255, 229, 221, 188, 154, 191, 210, 204, 209, 222, 228,
225, 0],
[ 98, 233, 198, 210, 222, 229, 229, 234, 249, 220, 194, 215, 217,
241, 65, 73, 106, 117, 168, 219, 221, 215, 217, 223, 223, 224,
229, 29],
[ 75, 204, 212, 204, 193, 205, 211, 225, 216, 185, 197, 206, 198,
213, 240, 195, 227, 245, 239, 223, 218, 212, 209, 222, 220, 221,
230, 67],
[ 48, 203, 183, 194, 213, 197, 185, 190, 194, 192, 202, 214, 219,
221, 220, 236, 225, 216, 199, 206, 186, 181, 177, 172, 181, 205,
206, 115],
[ 0, 122, 219, 193, 179, 171, 183, 196, 204, 210, 213, 207, 211,
210, 200, 196, 194, 191, 195, 191, 198, 192, 176, 156, 167, 177,
210, 92],
[ 0, 0, 74, 189, 212, 191, 175, 172, 175, 181, 185, 188, 189,
188, 193, 198, 204, 209, 210, 210, 211, 188, 188, 194, 192, 216,
170, 0],
[ 2, 0, 0, 0, 66, 200, 222, 237, 239, 242, 246, 243, 244,
221, 220, 193, 191, 179, 182, 182, 181, 176, 166, 168, 99, 58,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 40, 61, 44, 72, 41, 35,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0],
[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0]], dtype=uint8)
We can easily plot some of the random images in our training dataset.
# Plot an example image and its label
def plot_image(image_number=0):
plt.imshow(train_images[image_number], cmap=plt.cm.binary)
plt.title(class_names[train_labels[image_number]])
plt.axis(False)
# Plot five random images
plt.figure(figsize=(10, 1))
for i in range(5):
ax = plt.subplot(1, 5, i+1);
rand_index = random.choice(range(len(train_images)))
plot_image(image_number=rand_index)

Data Preprocessing
As I have described in my previous post on Feature preprocessing, we need to normalise or standardise our numerical dataset. This is required for creating Neural Networks, which work the best when we normalise or scale our input features.
# We can normalise the training and testing data
train_images_normalised = train_images / 255.0
test_images_normalised = test_images / 255.0
Multiclass Classification in TensorFlow
When we model neural networks in TensorFlow, we generally follow the steps:
- create a model and define the input, hidden and output layers, number of neurons in each layer;
- compile the model with required loss function, optimiser, evaluation metrics;
- fit the model for finding patterns between features and labels.
Creating Models
The model architecture consists of input, hidden, and output layers. The input layer shape is defined by the number of features, while the output layer shape is defined by the number of classes. Hidden layer activation is usually ReLU, but sometimes it is good to experiment with different activations. What is an activation function? You can read my previous post Artificial Neural Networks describing some of the most useful activation functions. Our output layer activation is Softmax, good for multiclass classification problems.
# Create a model
# Use tf.one_hot(train_labels, depth=10) and tf.one_hot(test_labels, depth=10)
# with CategoricalCrossentropy()
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(4, activation="relu"),
tf.keras.layers.Dense(4, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")])
In the model compilation step, we defined the loss function. The Adam optimiser (we could also try out an SGD optimiser) works on minimising the loss function, which ideally leads to better performance. Our labels are not encoded (labels are integers). This is why we use SparseCategoricalCrossentropy. Should we try to represent our labels with a one-hot encoder, we would use CategoricalCrossentropy.
# Compile the model
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(), metrics=["accuracy"])
Plotting the Model
We can see our model architecture using the plot_model function using tensorflow.keras.utils.
# Plotting deep learning models in TF
from tensorflow.keras.utils import plot_model
# See the inputs and outputs of each layer
plot_model(model, show_shapes=True)
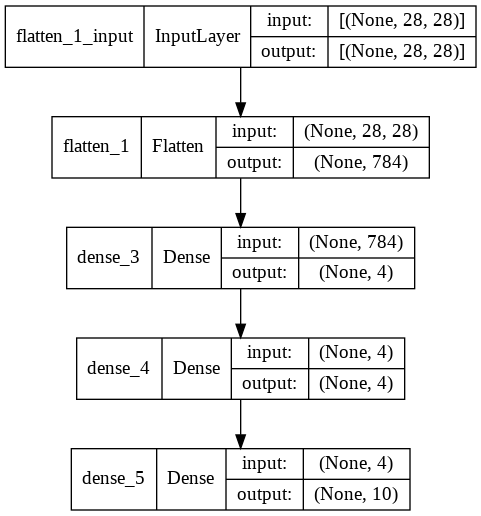
Optimising our Model
Even though the neural networks can work out-of-box with default parameters pretty well, it is necessary to ensure that we have the best settings of our network hyperparameters, and also the best architecture of our network.
To improve our model, we can do the following in any combination, however, performing minor adjustments to see whether this takes any effect on the model performance [1]:
- adding or removing layers;
- adding the number of hidden neurons;
- changing the activation function;
- changing the optimisation function;
- adjusting the learning rate (potentially, the most critical hyperparameter);
- adding more data;
- increasing the number of epochs;
In this post, we will focus on adjusting the learning rate with callbacks, and also define the number of epochs sufficient to get a well-performing model.
Finding the best learning rate with callbacks in training
During model training, we can add a callback with LearningRateScheduler to find out the best learning rate leading to the minimum loss function. The result of the model.fit() function is find_lr_history, which keeps the training results including loss function, accuracy for training and testing datasets. Please note that we added validation_data for evaluating the testing dataset.
# Create the learning rate callback
lr_scheduler = tf.keras.callbacks.LearningRateScheduler(lambda epoch: 1e-3 *10**(epoch/20))
# Fit the model
find_lr_history = model.fit(train_images_normalised, train_labels,
epochs=40, validation_data=(test_images_normalised,
test_labels), callbacks=[lr_scheduler], verbose=0)
The plot below shows the loss function with respect to the learning rate. We can find out which learning rate value results in the lowest loss value.
# Plot the learning rate decay curve
lrs = 1e-3 *(10**(tf.range(40)/20))
plt.semilogx(lrs, find_lr_history.history["loss"])
plt.xlabel("Learning Rate"); plt.ylabel("Loss");
plt.title("Finding the ideal learning rate");
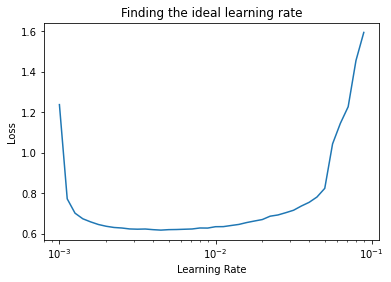
The argmin() function gives the index of the minimum loss value.
tf.argmin(find_lr_history.history["loss"])
<tf.Tensor: shape=(), dtype=int64, numpy=13>
The learning rate with the found index equals to .005, which we are going to use for building the final model.
find_lr_history.history["lr"][13]
0.004466836
# Draw the history plot with the learning rates
pd.DataFrame(find_lr_history.history).plot(figsize=(6, 4), xlabel="epochs");
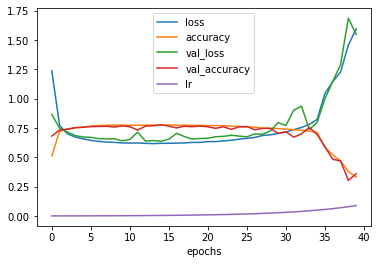
The maximum training accuracy equals about 0.8.
find_lr_history.history["accuracy"][13]
0.7751833200454712
Refitting the Model with the Best Learning Rate
In the previous step, we found out that the best learning rate for our model is .005, and the model requires 13 learning iterations.
# Create a model
# Use tf.one_hot(train_labels, depth=10) and tf.one_hot(test_labels, depth=10)
# with CategoricalCrossentropy()
model = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(4, activation="relu"),
tf.keras.layers.Dense(4, activation="relu"),
tf.keras.layers.Dense(10, activation="softmax")])
# Re-compile the model with the best learning rate we found
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(lr=0.005),
metrics=["accuracy"])
# Fit the model with the best number of epochs
history = model.fit(train_images_normalised, train_labels,
epochs=13, validation_data=(test_images_normalised,
test_labels), verbose=0)
/usr/local/lib/python3.7/dist-packages/keras/optimizer_v2/adam.py:105: UserWarning: The `lr` argument is deprecated, use `learning_rate` instead. super(Adam, self).__init__(name, **kwargs)
Prediction Probabilities
The model outputs prediction probabilities as a vector consisting of probabilities for each class label. The maximum probability corresponds to the class predicted. For instance, we predicted that the first item of our test data point corresponds to the class ‘Ankle boot.’
# Make some predictions
y_probs = model.predict(test_images_normalised)
# View the first prediction
y_probs[0], tf.argmax(y_probs[0]), class_names[tf.argmax(y_probs[0])], test_labels[0]
(array([8.8012495e-27, 7.6685532e-38, 0.0000000e+00, 1.0661165e-36,
0.0000000e+00, 3.2718729e-02, 1.4882749e-29, 4.4392098e-02,
4.4525089e-10, 9.2288911e-01], dtype=float32),
<tf.Tensor: shape=(), dtype=int64, numpy=9>,
'Ankle boot',
9)
Using argmax(), we convert prediction probabilities into integers, which is useful since the integers are related to the class label indexes.
# Convert all of the prediction probabilities into integers
y_preds = y_probs.argmax(axis=1)
# View the first 10 prediction labels
y_preds[:10]
array([9, 4, 1, 1, 6, 1, 6, 6, 5, 7])
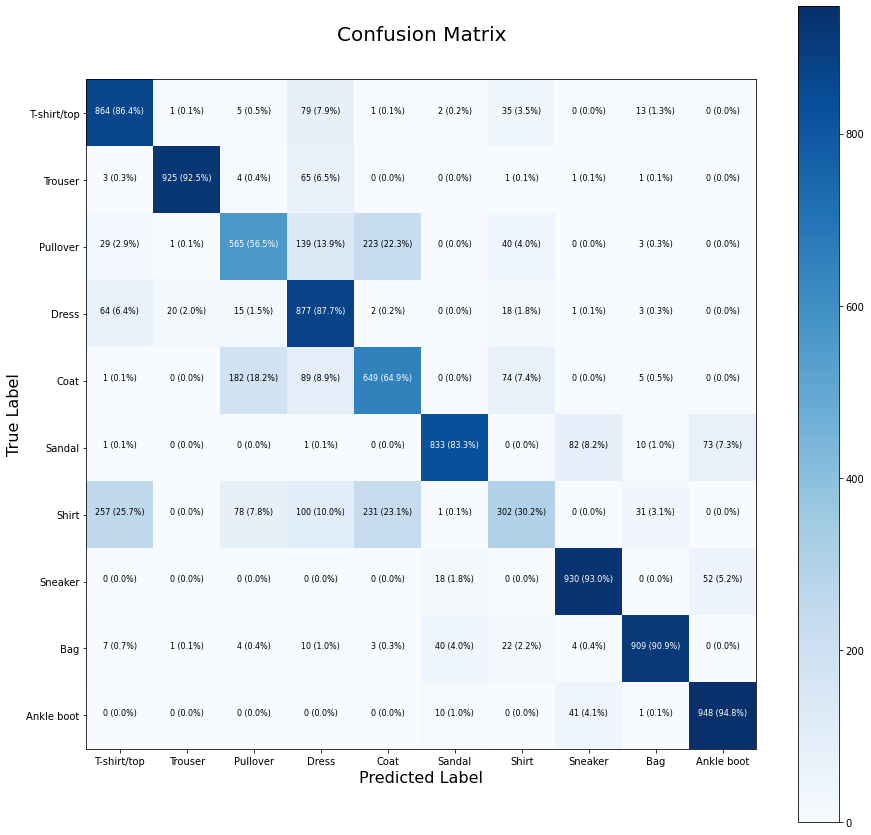
The following function provided in the Udemy course (referenced below) plots a confusion matrix. A confusion matrix is a technique used to visualise the quality of our predictive modeling, and it shows how the correspondence between ground truth and predicted labels. An ideal confusion matrix will have all values in its diagonal line.
# Plot Confusion Matrix
def plot_cm(y_test, y_preds, classes=None, figsize = (10, 10), text_size=16):
# Create the confusion matrix
cm = confusion_matrix(y_test, tf.round(y_preds))
# Normalise the confusion matrix
cm_normalised = cm.astype("float") / cm.sum(axis=1)[:, np.newaxis]
number_of_classes = cm.shape[0]
# Draw the plot
fig, ax = plt.subplots(figsize=figsize)
# Create a matrix plot
cax = ax.matshow(cm, cmap=plt.cm.Blues)
fig.colorbar(cax)
# Set labels to classes
if classes:
labels = classes
else:
labels = np.arange(cm.shape[0])
# Label the axes
ax.set(title="Confusion Matrix",
xlabel="Predicted Label",
ylabel="True Label",
xticks=np.arange(number_of_classes),
yticks=np.arange(number_of_classes),
xticklabels=labels,
yticklabels=labels
)
# Set x-axis labels to bottom
ax.xaxis.set_label_position("bottom")
ax.xaxis.tick_bottom()
# Adjust label size
ax.yaxis.label.set_size(text_size)
ax.xaxis.label.set_size(text_size)
ax.title.set_size(text_size+4)
# Set threshold for different colors
threshold = (cm.max() + cm.min()) / 2.
# Plot the text on each cell
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, f"{cm[i, j]} ({cm_normalised[i, j]*100:.1f})",
horizontalalignment="center",
color="white" if cm[i, j] > threshold else "black",
size=text_size/2)
plot_cm(test_labels, y_preds, figsize=(15, 15), classes=class_names)
Patterns Learned
When we train a Machine Learning model, we want it to automatically learn patterns allowing us to solve our problem, in our case, to classify fashion items. Neural network’ wights and biases are learned to get a well-performing model. Weights define the strength of the connection between neurons. Biases add constants to inputs to make the model better fit the data. We can get access to model layers as follows.
# Model layers
model.layers
[<keras.layers.core.flatten.Flatten at 0x7f3db77f3e50>, <keras.layers.core.dense.Dense at 0x7f3db77f32d0>, <keras.layers.core.dense.Dense at 0x7f3db78446d0>, <keras.layers.core.dense.Dense at 0x7f3db7796c50>]
# Extract a particular layer
model.layers[1]
<keras.layers.core.dense.Dense at 0x7f3db77f32d0>
Each layer has weights, and biases learned during model training.
# Get the patterns of the layer
weights, biases = model.layers[1].get_weights()
# weights and their shape
weights, weights.shape
(array([[ 0.00711583, 0.18802351, -0.92773247, -0.03165132],
[ 1.6469412 , 2.1759915 , -1.6559064 , -0.13926847],
[ 1.6107311 , 1.6976608 , -1.2488168 , -1.0657196 ],
...,
[ 0.38724658, 3.3352914 , 0.02761855, -0.6212328 ],
[ 1.2829345 , 1.7459874 , 1.9171976 , 1.2210226 ],
[-0.04135585, 1.1622185 , 0.5536791 , 0.8744017 ]],
dtype=float32), (784, 4))
# Bias and biases' shape
biases, biases.shape
(array([1.4261936, 2.5197918, 3.2453992, 4.0508494], dtype=float32), (4,))
Conclusion
In this post, I have described the multiclass classification problem using Fashion MNIST dataset. With training callback, we have identified the best learning rate. To assess the accuracy of our classification model, we draw some learning curves and a confusion matrix. We also saw how to access learned patterns for our model layers.
Try the following fantastic AI-powered applications.
I am affiliated with some of them (to support my blogging at no cost to you). I have also tried these apps myself, and I liked them.
B12.io Recently, I have found an AI-powered platform that enables you to create professional websites, pages, posts, and emails with ease. I will also give it a try and soon write a new post about B12.io (I am working on my coding post at the moment :).
UseBasin.com is a comprehensive backend automation platform for handling submissions, processing, filtering, and routing without coding.
Mixo.io generates websites instantly using AI. Builds stunning landing pages without any code or design. Includes a built-in email waiting list and all the tools you need to launch, grow, and test your ideas.
10web.io builds a website with AI. You can also host your wesbite on 10Web Hosting, and optimise it with PageSpeed Booster.
Did you like this post? Please let me know if you have any comments or suggestions.
Python posts that might be interesting for youThanks
For writing this post, I have used TensorFlow documentation and tutorials at Udemy, TensorFlow Developer Certificate in 2022: Zero to Mastery.

|
About Elena Elena, a PhD in Computer Science, simplifies AI concepts and helps you use machine learning.
|